Curve Functions

Functions that work with forward curves

abs

Transforms all values of the input variable to absolute (positive) values.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

abs(var)

Examples

Timeseries

at = TimeSeries("DAILY")
at.add("2020-11-01", 12.5)
at.add("2020-11-02", -12.75)
at.add("2020-11-03", 12.9)
at.add("2020-11-04", -11.5)
at.add("2020-11-05", 11.9)
absat = abs(at)
print absat.values

[
  {"2020-11-01": 12.5},
  {"2020-11-02": 12.75},
  {"2020-11-03": 12.9},
  {"2020-11-04": 11.5},
  {"2020-11-05": 11.9}
]

List

testarray = [-1,6,0,-2]
print abs(testarray)

Curve

expiry = ExpiryCalendar(BusinessCalendar())
expiry.addRule("go back 1 day using calendar")
ondate = CurveDate(Date("2020-12-01"), expiry)
c1 = Curve(ondate)
c1.add(Contract(ondate, "2021M01", 12.5))
c1.add(Contract(ondate, "2021M02", -12.75))
c1.add(Contract(ondate, "2021M03", 13.0))
print abs(c1)

Scalar

print abs(-2)

2

acos

Returns the arc cosine of a value; the returned angle is in the range 0.0 through pi.

Special case: If the argument is NaN or its absolute value is greater than 1, then the result is NaN.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

acos(var)

asin

Returns the arc sine of a value; the returned angle is in the range -pi/2 through pi/2.

Special cases:

• If the argument is NaN or its absolute value is greater than 1, then the result is NaN.
• If the argument is zero, then the result is a zero with the same sign as the argument.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

asin(var)

asDays

A curve function that breaks a single contract into a list of daily contracts, e.g. a month into days

Syntax

Contracts = asDays(Contract)

Result

A Contracts object

Example

c = Contract(ondate, "2021M01", 26.85)
contracts = asDays(c)
for tenor in contracts
    print tenor.absolute + " : " + tenor.value
next

asHours

A curve function that breaks a single contract into a list of hours contracts, e.g. a day into hours

Syntax

Contracts = asHours(Contract)
Contracts = asHours(Contract, Timezone)

Result

A Contracts object, if a timezone is specified, all the hours will be in the specified timezone.

Example

function hourly(input, timezone)
    hourly = Curve(input.ondate)
    hourly.timezone = timezone
    for pc in input.contracts
        hourly.add(asHours(pc, timezone))
    next
end

asMonths

A curve function that breaks a single contract into a list of monthly contracts, e.g. a quarter into 3 months

Syntax

Contracts = asMonths(Contract)

Result

A Contracts object

Example

c = Contract(ondate, "2021Q01", 26.85)
contracts = asMonths(c)
for tenor in contracts
    print tenor.absolute + " : " + tenor.value
next

2021M01 : 26.85
2021M02 : 26.85
2021M03 : 26.85

asStrips

Creates an arbitrage free curve comprised of calendar year strips

Syntax

c = asStrings(curve)

Result

A curve containing only calendar year contracts.

Example

c = asStrips(curve)
print c

atan

Returns the arc tangent of a value; the returned angle is in the range -pi/2 through pi/2.

Special cases:

• If the argument is NaN or its absolute value is greater than 1, then the result is NaN.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

atan(var)

atan2

Returns the angle theta from the conversion of rectangular coordinates (x, y) to polar coordinates (r, theta). This method computes the phase theta by computing an arc tangent of y/x in the range of -pi to pi.

Special cases:

• If either argument is NaN, then the result is NaN.
• If the first argument is positive zero and the second argument is positive, or the first argument is positive and finite and the second argument is positive infinity, then the result is positive zero.
• If the first argument is negative zero and the second argument is positive, or the first argument is negative and finite and the second argument is positive infinity, then the result is negative zero.
• If the first argument is positive zero and the second argument is negative, or the first argument is positive and finite and the second argument is negative infinity, then the result is the double value closest to pi.
• If the first argument is negative zero and the second argument is negative, or the first argument is negative and finite and the second argument is negative infinity, then the result is the double value closest to -pi.
• If the first argument is positive and the second argument is positive zero or negative zero, or the first argument is positive infinity and the second argument is finite, then the result is the double value closest to pi/2.
• If the first argument is negative and the second argument is positive zero or negative zero, or the first argument is negative infinity and the second argument is finite, then the result is the double value closest to -pi/2.
• If both arguments are positive infinity, then the result is the double value closest to pi/4.
• If the first argument is positive infinity and the second argument is negative infinity, then the result is the double value closest to 3*pi/4.
• If the first argument is negative infinity and the second argument is positive infinity, then the result is the double value closest to -pi/4.
• If both arguments are negative infinity, then the result is the double value closest to -3*pi/4.

The computed result must be within 2 ulps of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

atan2(ordinate, abscissa)

bootstrapCurve

Creates an arbitrage free monthly curve from an input curve

Description

The bootstrap function converts quarters, seasons and years into months and performs an arbitrage-free calculation on any overlapping periods.

Syntax

bootstrapped = bootstrapCurve(Curve)

Result

A curve with monthly tenors

Example

ondate = CurveDate(Date("2020-12-14"), "REOMHENG")

curve = Curve(ondate)
curve.add(Contract(ondate, "2021M01", 26.87))
curve.add(Contract(ondate, "2021Q01", 26.85))
curve.add(Contract(ondate, "2021Q02", 26.75))

bootstrapped = bootstrapCurve(curve)
for tenor in bootstrapped.contracts
    print tenor.absolute + " : " + tenor.value
next

2021M01 : 26.87
2021M02 : 26.84
2021M03 : 26.84
2021M04 : 26.75
2021M05 : 26.75
2021M06 : 26.75

You can see in the example that 2021M02 and 2021M03 are calculated using the formula:

((2021Q01 * 3) - 2021M01) / 2

cbrt

Returns the cube root of a double value. For positive finite x, cbrt(-x) == -cbrt(x); that is, the cube root of a negative value is the negative of the cube root of that value's magnitude.

Special cases:

• If the argument is NaN, then the result is NaN.
• If the argument is infinite, then the result is an infinity with the same sign as the argument.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

cbrt(var)

combine

Combines 2 curves into 1 - uses the date and expiry calendar from the base

Syntax

curve = combine(base, other, replace)

Replace:

• true - matching tenors from the base are overwritten
• false - only new tenors in other are added to the base

Example

print combine(BASE, OTHER, true)

cos

Returns the trigonometric cosine of an angle.

Special cases:

• If the argument is NaN or an infinity, then the result is NaN.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

cos(var)

cosh

Returns the hyperbolic cosine of a double value. The hyperbolic cosine of x is defined to be (ex + e-x)/2 where e is Euler's number.

Special cases:

• If the argument is NaN, then the result is NaN.
• If the argument is infinite, then the result is positive infinity.
• If the argument is zero, then the result is 1.0.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

cosh(var)

exp

Returns Euler's number e raised to the power of a double value.

Special cases:

• If the argument is NaN, the result is NaN.
• If the argument is positive infinity, then the result is positive infinity.
• If the argument is negative infinity, then the result is positive zero.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

exp(var)

extendCurve

Extends a curve by a required number of years by using the value of the last maturity

Syntax

extended = extendCurve(curve, years)

The years parameter represents the number of years to extend the curve by. For example, if a curve ends in May 2022 and you specify 2 for years, the curve will be extends to December 2024.

Example

function agricultural(input)
    // Agricultural curve forward filled and extended to end of 3 years
    filled = forwardFillCurve(input)
    extended = extendCurve(filled, 3)
    agricultural = shape(extended)
end

forwardFillCurve

Fills any gaps in a curve by using the value from a previous maturity

Syntax

filled = forwardFillCurve(curve)

Result

The function checks for any gaps in the maturities of a curve and forward fills using the value of the maturity immediately before it.

Example

ondate = CurveDate(Date("2020-10-30"), "REOMHENG")

curve = Curve(ondate)
curve.add(Contract(ondate, "2020M11", 26.87))
curve.add(Contract(ondate, "2020M12", 26.85))
curve.add(Contract(ondate, "2021M01", 26.75))
curve.add(Contract(ondate, "2021M03", 26.62))
curve.add(Contract(ondate, "2021M04", 26.55))

filled = forwardFillCurve(curve)

for tenor in filled.contracts
    other = curve\[tenor.tenor\]
    if other
        print tenor.tenor + " = " + tenor.value + " was " + other.value
    else
        print tenor.tenor + " = " + tenor.value
    end
next

This produces the following output:

M00 = 26.870000 was 26.870000
M01 = 26.870000 was 26.850000
M02 = 26.750000 was 26.750000
M03 = 26.750000
M04 = 26.620000 was 26.620000
M05 = 26.550000 was 26.550000

log

Returns the natural logarithm (base e) of a double value.

Special cases:

• If the argument is NaN or less than zero, then the result is NaN.
• If the argument is positive infinity, then the result is positive infinity.
• If the argument is positive zero or negative zero, then the result is negative infinity.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

log(var)

log10

Returns the base 10 logarithm of a double value.

Special cases:

• If the argument is NaN or less than zero, then the result is NaN.
• If the argument is positive infinity, then the result is positive infinity.
• If the argument is positive zero or negative zero, then the result is negative infinity.
• If the argument is equal to 10n for integer n, then the result is n.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

log10(var)

log1p

Returns the natural logarithm of the sum of the argument and 1. Note that for small values x, the result of log1p(x) is much closer to the true result of ln(1 + x) than the floating-point evaluation of log(1.0+x).

Special cases:

• If the argument is NaN or less than -1, then the result is NaN.
• If the argument is positive infinity, then the result is positive infinity.
• If the argument is negative one, then the result is negative infinity.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

log10(var)

pow

Returns the value of the first argument raised to the power of the second argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

pow(base, exponent)

shape

A curve function that shapes a monthly curve

Syntax

Curve = shape(Curve)

Result

A curve that is shaped using the a normalised shape based on the first 12 months of the input curve. It then shapes the rest of the curve in blocks of 12 months retaining the correct average values.

Example

ondate = CurveDate(Date("2020-10-30"), "REOMHENG")

curve = Curve(ondate)
curve.currency = "EUR"
curve.units = "MWH"
curve.add(Contract(ondate, "2020M11", 26.87))
curve.add(Contract(ondate, "2020M12", 26.85))
curve.add(Contract(ondate, "2021M01", 26.75))
curve.add(Contract(ondate, "2021M02", 26.65))
curve.add(Contract(ondate, "2021M03", 26.62))
curve.add(Contract(ondate, "2021M04", 26.55))
curve.add(Contract(ondate, "2021M05", 26.68))
curve.add(Contract(ondate, "2021M06", 26.89))
curve.add(Contract(ondate, "2021M07", 27.05))
curve.add(Contract(ondate, "2021M08", 27.15))
curve.add(Contract(ondate, "2021M09", 27.02))
curve.add(Contract(ondate, "2021M10", 26.85))
curve.add(Contract(ondate, "2021Q04", 26.92))
curve.add(Contract(ondate, "2022Y", 27.12))
curve.add(Contract(ondate, "2023Y", 27.20))

bootstrapped = bootstrapCurve(curve)
shaped = shape(bootstrapped)

for tenor in shaped.contracts
    print tenor.absolute + " : " + tenor.value
next

2020M11 : 26.870000
2020M12 : 26.850000
2021M01 : 26.750000
2021M02 : 26.650000
2021M03 : 26.620000
2021M04 : 26.550000
2021M05 : 26.680000
2021M06 : 26.890000
2021M07 : 27.050000
2021M08 : 27.150000
2021M09 : 27.020000
2021M10 : 26.850000
2021M11 : 26.955000
2021M12 : 26.955000
2022M01 : 27.025839
2022M02 : 26.924628
2022M03 : 26.894362
2022M04 : 26.823741
2022M05 : 26.954893
2022M06 : 27.167080
2022M07 : 27.328824
2022M08 : 27.429710
2022M09 : 27.298558
2022M10 : 27.126726
2022M11 : 27.232819
2022M12 : 27.232819
2023M01 : 27.105562
2023M02 : 27.004051
2023M03 : 26.973696
2023M04 : 26.902867
2023M05 : 27.034406
2023M06 : 27.247219
2023M07 : 27.409440
2023M08 : 27.510624
2023M09 : 27.379085
2023M10 : 27.206746
2023M11 : 27.313152
2023M12 : 27.313152

This is the bootstrapped curve:

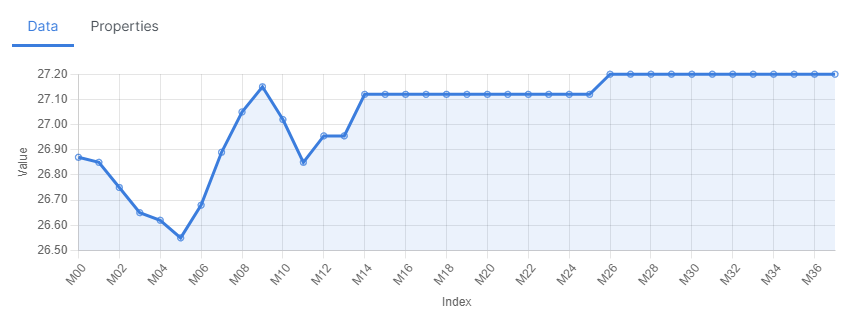
And here is the shaped curve:

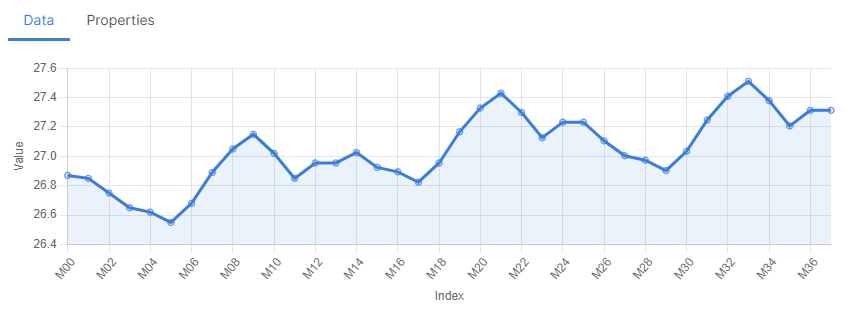
sin

Returns the trigonometric sine of an angle.

Special cases:

• If the argument is NaN or an infinity, then the result is NaN.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

sin(var)

sinh

Returns the hyperbolic sine of a double value. The hyperbolic sine of x is defined to be (ex - e-x)/2 where e is Euler's number.

Special cases:

• If the argument is NaN, then the result is NaN.
• If the argument is infinite, then the result is an infinity with the same sign as the argument.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

sinh(var)

sqrt

Returns the correctly rounded positive square root of a double value.

Special cases:

• If the argument is NaN or less than zero, then the result is NaN.
• If the argument is positive infinity, then the result is positive infinity.
• If the argument is positive zero or negative zero, then the result is the same as the argument.
• Otherwise, the result is the double value closest to the true mathematical square root of the argument value.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

sqrt(var)

tan

Returns the trigonometric tangent of an angle.

Special cases:

• If the argument is NaN or an infinity, then the result is NaN.
• If the argument is zero, then the result is a zero with the same sign as the argument.

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

tan(var)

tanh

Returns the hyperbolic tangent of a double value. The hyperbolic tangent of x is defined to be (ex - e-x)/(ex + e-x), in other words, sinh(x)/cosh(x). Note that the absolute value of the exact tanh is always less than 1.

Special cases:

• If the argument is NaN, then the result is NaN.
• If the argument is zero, then the result is a zero with the same sign as the argument.
• If the argument is positive infinity, then the result is +1.0.
• If the argument is negative infinity, then the result is -1.0.

The computed result must be within 2.5 ulps of the exact result. The result of tanh for any finite input must have an absolute value less than or equal to 1. Note that once the exact result of tanh is within 1/2 of an ulp of the limit value of ±1, correctly signed ±1.0 should be returned.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

tanh(var)

toDegrees

Converts an angle measured in radians to an approximately equivalent angle measured in degrees. The conversion from radians to degrees is generally inexact; users should not expect cos(toRadians(90.0)) to exactly equal 0.0.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

toDegrees(var)

toRadians

Converts an angle measured in degrees to an approximately equivalent angle measured in radians. The conversion from degrees to radians is generally inexact.

Works with:

• Scalars
• Timeseries
• Curves
• Lists/Arrays

Syntax

toRadians(var)